Известно, что при приложении к p-n-переходу обратного напряжения с каждой его стороны возникает обеднённый подвижными носителями заряда слой. Его суммарная толщина для ступенчатого перехода:

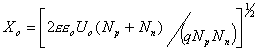	(17)
для плавного перехода:
	(18)

В выражениях (17) и (18) Х₀ - суммарная толщина обеднённого слоя, см; e - относительная диэлектрическая проницаемость полупроводника (для кремния при Т=300К e=11,7); e₀=8,85×10^-14 Ф/см - диэлектрическая проницаемость вакуума; U₀ - обратное напряжение на переходе, В; N_p и N_п - эффективные концентрации примесей на соответствующих сторонах перехода, см^-3; q=1,6×10^-19 Кл - заряд электрона; а - градиент концентрации, см^-4 , на глубине Х=Х_п.

Плавные переходы (монотонное изменение концентрации примеси в окрестностях перехода) возникают при формировании областей методом термической диффузии примеси, а также в донной части имплантированных областей. На боковых границах имплантированных областей образуются ступенчатые переходы.

Из выражений (17) и (18) следует, что с ростом обратного напряжения U₀ напряжённость поля в обедненном слое Е= U₀/ X₀ возрастает и при достижении критического значения Е_max (для кремния 3×10⁵ В/см) наступает лавинный пробой. Соответствующее напряжение U₀ называют пробивным напряжением U_пр:

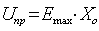(19)

Из (17) и (18) с учётом (19) можно получить формулы пробивного напряжения для ступенчатого перехода:

	(20)
и для плавного перехода:
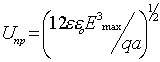	(21)

Градиент концентрации a представляет собой первую производную от функции распределения примеси, вычисленную при значении Х=Х_п (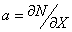 | x=x_п).

Градиент эффективной (иначе некомпенсированной, избыточной) примеси определяется как алгебраическая разность между градиентом концентрации введённой примеси и градиентом эффективной концентрации в исходной области.

Градиент концентрации введённой примеси при двухстадийной диффузии (гауссово распределение):

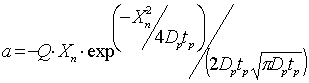	(22)
При одностадийной диффузии (закон дополнения функции ошибок):
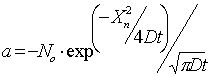	(23)

Выражение (22) справедливо для донной (плоской) части перехода. Для боковой радиусной части перехода на поверхности следует использовать формулу (23) с подстановкой вместо N₀ значения 0,5N₀₃, где N₀₃ - поверхностная концентрация примеси на этапе загонки.

При ионной имплантации (гауссово распределение):

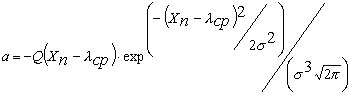(24)

В выражения (18) и (21) входят абсолютные значения величины а.

Так как реальная кристаллическая решётка содержит дефекты, расчётное значение U_пр должно превышать приложенное обратное напряжение U₀ в 3-4 раза.