ВВЕДЕНИЕХорошо известно, что квантовая механика построена на невозможности точно измерить определенные параметры физического мира, как, например, скорость и координаты частицы. В подобной ситуации результат измерения параметров непредсказуем, поскольку экспериментатор самим фактом наблюдения непредсказуемо изменяет параметры системы Рассмотрим провод, по которому течет неопределенный сигнал с вероятностью половина - единица, с вероятностью половина-ноль. Такой сигнал кубитом, т. е. квантовым битом. Сто квантовых бит, текущих по проводу, несут сигнал, с равной принимающий значения от нуля до астрономического числа 2^100. Пусть удалось сконструировать машину, производящую сигнал в 100 кубит . Тогда нетрудно построить компьютер, мгновенно решающий любую заданную наперед криптографическую задачу. Я поясню это на простом примере. Пусть задано число x порядка 2200,и необходимо определить, простое ли оно. Детерминистский (неквантово-механический) компьютер, способный это сделать, будет весить больше, чем вся Солнечная система. А с помощью провода, по которому подается сигнал в 100 кубит, определить, простое ли х, ничего не стоит. Пусть у нас есть механизм, лишенный любых квантовых неопределенностей (т. е. просто железка), который делит x на y и выдает на провод сигнал 1, если делится, и 0, когда не делится. Подадим на входе этому механизму сигнал в 100 кубит. Эффект будет таким же, как если бы мы подавали все числа от 0 и до 2100 одновременно, а результат будет среднеарифметическим (суперпозицией) нулей и единиц, полученных в каждом и случаев. Короче говоря, на выходе будет 0 если х простое, и очень маленький ненулевой сигнал, если х составное. Усилив этот сигнал, узнаем, составное или простое число х. Открытие алгоритмов квантовых вычислений, обеспечивающих решение ряда классических задач за эскпоненциально меньшее число элементарных операций (в зависимости от числа битов, необходимых для записи входных параметров) привлекло большое внимание к исследованию квантовых компьютеров не только как к нетривиальным объектам академической науки, но и как к возможным конкурентам классических компьютеров в области решения классически .трудных. задач. В настоящее время осуществлены простейшие модели такого рода компьютеров, включающие в себя два-три элементарных квантовых бита (q-бита), никоим образом не опережающие по вычислительной мощи обычные ЭВМ. Осуществление квантового компьютера на многих q-битах оказалось сложной экспериментальной задачей. Дело в том, что требования квантовой когерентности, то есть слабости взаимодействия с декогерентизующей внешней средой . источником помех и ошибок, и управляемости, то есть хорошего отклика (изменения состояния) q- битов на внешние управляющие сигналы, достаточно трудно совместить в эксперименте. До сих пор неясно, на каких же физических структурах он будет построен. В силу этого, для анализа различных физических систем . кандидатов в квантовые компьютеры необходимо сформулировать набор требований, необходимых для практической реализации конкурентоспособного компьютера. Это позволит отсеивать негодные системы и сконцентрировать внимание на перспективных физических объектах. Из известных квантовых алгоритмов практический интерес (и наибольшее ускорение вычислений) представляют, прежде всего, моделирование квантовой динамики большого числа взаимодействующих частиц и алгоритм Шора (разложение больших чисел на множители). Первая задача менее конкретна, поскольку множество физических систем достаточно широко и разнообразно. Целью такого рода моделирования должен, вероятно, являться поиск новых эффектов или проверка сложных физических моделей, требующих учета весьма тонких деталей квантового взаимодействия. По-видимому, для получения качественно новых результатов, не достигнутых в квантовой теории, точном численном моделировании динамики малого числа частиц и приближенном моделировании большого числа частиц на обычных компьютерах, необходимо рассматривать достаточно большое (порядка нескольких сотен) число частиц. Окажется ли квантовый компьютер с заданного размера квантовым регистром эффективным для решения такого рода задачи, будет зависеть не только от длины регистра, но и от особенностей конкретной физической системы, которую предстоит моделировать. Алгоритм разложения чисел на множители лучше подходит для оценки возможностей квантового компьютера, так как сформулирован предельно конкретно. Начнем с описания поставленной задачи : факторизации числа N на простые множители (например число 51688 может быть разложено, как 2^3 х 7 х 71) Для того чтобы оценить ,как быстро конкретный алгоритм может решить задачу ,состоит в том ,чтобы выяснить как число шагов , требуемых для выполнения алгоритма ,растет с увеличением размера входных данных. Для задачи факторизации входными данными является само число N ,которое мы хотим факторизовать,то есть длина входа - log N. Эфективными считаются алгоритмы в которых число шагов растет как некоторый полином небольшой степени (2 или 3)от размера входных данных. На обычных компьютерах самые лучшие алгоритмы факторизации выполняются за О(exp[(64/9^1/3 )*(ln ln N)^2/3)]) шагов . Таким образом число шагов растет экспоненциально ,с размером входных данных log N, что является совершенно неприемлемым. Например,в 1994 году 129-значное число (известное, как RSA 129) было успешно разложено с использованием примерно 1600 компьютеров , распределенных по всему миру, это заняло 8 месяцев. ри использовании того же алгоритма , для факторизации теми же компьютерами 250-значного числа понадобиться примерно 8* 10^5 лет , для 1000-значного числа -порядка 10^25 лет (значительно больше ,чем возраст вселенной) Трудность факторизации больших числе является определяющим фактором для криптосистем с открытым ключом, типа RSA. Недавно был разработан алгоритм для факторизации чисел на квантовом компьютере , который реализуется за О((log N)^2+e)) шагов, где e -некое малое число. Он приблизительно квадратично зависит от размера входных данных поэтому факторизация 1000-значного числа потребует только несколько миллионов шагов. Это значит что криптосистемы с открытым ключом , основанные на факторизации ,могут быть взломаны. Немного о криптографии RSA (Rivest-Shamir-Adleman) - криптография с открытым ключомАлгоритм RSA -- ассиметричный, т. е. для шифрования и расшифрования используются разные ключи. Любой из ключей может быть открытым, т. е. кто угодно сможет зашифровать текст, но расшифровать -- только тот, кто знает секретный ключ (хорошие системы парольной идентификации -- пароли хранятся в зашифрованном виде, ввод шифруется и сравнивается с паролем -- т. е. даже полностью разобравшись в логике шифратора нельзя узнать исходный пароль, т. к. ключ для расшифрования будет физически отсутствовать) или, наоборот, прочитать текст может каждый, но зашифровать -- только один человек (системы подтверждения подлинности; программы, зашифрованный код которых нельзя изменить, даже зная алгоритм шифрования). Вот краткое изложение алгоритма:
Шифрование происходит так:
Криптостойкость алгоритма основана на предположении, что не существует эффективного способа разложения числа на простые множители. С другой стороны, пока нельзя гарантировать, что таких способов не появится в будущем. Так как криптостойкость основана сложности разложения на множители, рекомендуется использовать в качестве ключей достаточно большие числа -- 256--512 двоичных разрядов (для достижения надежности DES необходимо применять около 700 двоичных разрядов). Для достижения хорошей секретности, кроме того, необходимо, чтобы числа (P-1) и (Q-1) имели большие простые делители (т. е. число 2X+1 является "плохим"). Кроме того, при регулярном использовании алгоритма, лучше, если у разных ключей будут отличаться оба числа в паре (т. е. нежелательно использовать ключи (E1,N) и (E2,N) или (E,N1) и (E,N2)). На сегодняшний день RSA является самым распространенным криптографическим алгоритмом с открытым ключом. El Gamal - еще один ассиметричный алгоритмСистема, предложенная Эль Гамалем, является, как и RSA, системой с открытым ключом. Ее криптостойкость основана на трудоемкости вычисления дискретного логарифма (т. е. трудоемкости операции логарифмирования в целых числах по модулю N). Ключи строятся так:
Шифрование блока B протекает следующим образом (открытый ключ):
Расшифрование протекает следующим образом (секретный ключ):
Логика квантового компьютера
Теория Гейты с точки зрения квантовой механики.
Примеры практической реализации Физические реализации квантового компьютера
Квантовые системы Информацию о семинаре по квантовым вычислениям, проводимом еженедельно по вторникам в Физико-технологическом институте РАН (Москва), можно найти на сайте: http://qc.ipt.ac.ru/ Там же можно узнать о работе лаборатории квантовых компьютеров в этом институте. Борьба за когерентность
Другим направлением является изобретение таких систем квантового компьютера, которые устойчивы к воздействиям внешнего окружения. Основным параметром, по которому сравниваются предлагаемые сейчас конструкции квантового компьютера является количество логических операций, производимых за время нарушения когерентности. На этом пути находится использование в качестве кубитов коллективных (макроскопических) состояний, например, сверхпроводящие кольца или неабелевы анионы, возможно проявляющиеся в дробном квантовом эффекте Холла. В последнее время появилось понятие подпространств, свободных от декогеренизации (Decoherence Free Subspace). Проблема состоит в том, как сохранять состояния в этом гильбертовом подпространстве и как производить вычисления и измерять результат. Ученые из University of California, Berkeley (США) предлагают общую схему проведения универсальных квантовых вычислений в DFS [1]. Логический кубит представляется в виде кластера из четырех DFS кубитов. Это позволяет подавить декогеренизацию, вызываемую пространственно коррелированным шумом. В реальных твердотельных структурах квантового компьютера в качестве такого шума могут выступать фононы. Сохранение когерентного состояния, по предложению авторов, основано на запретах, связанных с сохранением симметрии состояния. В качестве примера рассмотрена структура квантового компьютера, основанного на обменном взаимодействии спинов. Запреты по симметрии используются в конструкции квантового компьютера, предложенного В.В.Вьюрковым (ФТИАН, Москва) и Л.Ю.Гореликом (Chalmers University, Goteborg, Швеция) [2]. В кубите из 4-х квантовых точек подавлена декогеренизация, связанная с флуктуациями напряжения на управляющих электродах. Ученые из Imperial College London и Universitat-GHS Essen (Германия) предлагают использовать квантовый эффект Зенона, вызванный взаимодействием с внешней средой [3]. Сильное взаимодействие со средой, подобно постоянному измерению, “загоняет” систему в область DFS. В качестве конкретного примера рассмотрен компьютер на атомных цепочках. С оригинальной идеей выступил югославский ученый M.Dugic [4]. Он предлагает не подавлять декогерентность системы компьютера, а усиливать релаксацию среды, “загоняющую” ее в основное состояние. Ясно, что без изменения состояния среды не может измениться состояние и системы компьютера.
Квантовый компьютер. Для тех, кто
еще не понял… Принцип работы такого компьютера связан с таинственными и пока непостижимыми для большинства людей квантовыми свойствами атомов и других частиц. Квантовый компьютер, в частности, может быть основан на спинах электронов и атомных ядер и на странных свойствах квантовых частиц в момент, когда их не наблюдают, иметь спин одновременно разных направлений. Когда спин частицы направлен вверх, атом может быть "считан" как 1, а направление вниз будет соответствовать 0. Это аналогично традиционному транзистору, в котором нули и единицы соответствуют включенному и выключенному состояниям, промежуточных состояний у классического бита не бывает. Но что делает квантовый компьютер уникальным, так это тот факт, что квантовые частицы, даже будучи очень хорошо изолированными друг от друга, могут находиться в запутанном состоянии (entangled state), в котором частицы все-таки зависят друг от друга. В классическом компьютере изменение состояния отдельного бита никак не связано с изменением состояния всех остальных битов, разве что только одного. В квантовом компьютере управление состоянием одной частицы вызывает изменение состояния всех других. Это и приводит к т.н. квантовому параллелелизму вычислений. Благодаря этому эффекту квантовый компьютер может иметь феноменальную производительность. Для определенных типов вычислений, подобных сложным алгоритмам для криптографии или поискам в гигантских массивах данных, квантовый компьютер может использовать "в тандеме" сотни атомов. На классическом компьютере это бы соответствовало выполнению миллиардов операций одновременно. "АйБиэМовский" тестовый образец квантового компьютера, в котором "работают" пока всего пять атомов в режиме и процессора, и памяти, впервые в мире показал свой истинный потенциал. При решении определенных задач его скорость заметно больше, чем в традиционных компьютерах. Эту экспериментальную машину можно рассматривать как существенный шаг к принципиально новому классу машин, способных к сверхбыстрым вычислениям. Isaac Chuang, исследователь из IBM, который возглавляет совместную группу ученых из IBM, Stanford Univ. и Univ. Calgary, утверждает, что квантовый компьютер можно будет использовать и для вполне прагматических целей, помимо специальных, например, для поиска в базах данных (в частности, в больших массивах Интернета). Более специальное использование – криптография (создание и раскрытие кодов). В таком использовании особенно заинтересованы Агентство национальной безопасности и Министерство обороны США, обильно финансирующие разработки квантового компьютера в Stanford Univ. В соответствии с пресловутым законом Мура (пока действующим неукоснительно!) в ближайшее десятилетие ожидается достижение предела в дальнейшем уменьшении размеров элементов традиционных полупроводниковых ИС. "С началом эпохи квантового компьютера закону Мура придет конец. И это наступит около 2020 года, когда размер электронных схем станет измеряться размерами атомов и молекул, которые составят элементную базу квантового компьютера" – утверждает Isaac Chuang. Он же сообщает, что его группа использует АйБиэМовский тестовый квантовый компьютер для решения некоторых математических задач криптографии, например, нахождения периода функций. Квантовый компьютер способен решать задачи в один цикл, в то время как традиционному компьютеру для этих же целей понадобились бы многократные циклы. Первые эксперименты демонстрируют жизнеспособность тестовой модели квантового компьютера, правильность выбранного пути его конструирования, соответствие задуманного и предсказанного реальным экспериментальным параметрам. Пока не ясно, когда же такой компьютер станет коммерческим изделием. Isaac Chuang считает, что компьютер, использующий в тандеме 7-10 атомов, появится в ближайшие 2 года. Из сообщений Агентства Reuter 14.08.00
Основными состояниями кубита является нахождение электрона в одной из двух соседних квантовых нитей. Любая квантовая суперпозиция этих состояний возникает за счет туннелирования электрона из одной нити в другую. Прозрачность потенциального барьера управляется внешним электродом. На рисунке представлен переход первичного волнового пакета из левой нити в правую (за 320фс) и назад по мере продвижения пакета вдоль оси нити y. Исходный волновой пакет имел пространственный размер поперек нити 50нм и вдоль нити 10нм, средняя энергия электрона полагалась равной 0.1эВ. Операция контролируемого НЕ (CNOT) осуществляется за счет кулоновского взаимодействия электронов, принадлежащих разным кубитам, на некотором промежутке, где соответствующие квантовые нити близко подходят друг к другу. Эта операция также осуществляется за весьма короткое время – 400фс. Соответствующие картинки в статье тоже приведены. Налюбовавшись на картинку, постараемся заметить и недостатки работы. Во-первых, не ясно, откуда можно взять одинаковые и столь узкие в пространстве электронные волновые пакеты. Во-вторых, пакеты значительно уширяются после каждой операции над кубитом (перекачивания из одной нити в другую). Из-за этого точность выполнения операции CNOT значительно падает, поскольку кулоновское взаимодействие ослабляется. Хоть авторы и утверждают, что изготовление структуры возможно с помощью современной технологии, конкретная конструкция компьютера отсутствует
Кулоновский компьютер без перемещения заряда
Теперь, похоже, преодолено и второе препятствие. В.Вьюрков (ФТИАН) и Л.Горелик (Chalmers University, Goteborg, Швеция) предложили конструкцию квантового компьютера на квантовых точках, основанного на пространственных (зарядовых) состояниях электронов. В этой конструкции перемещение заряда не происходит, а, следовательно, отсутствует непредсказуемое кулоновское взаимодействие кубитов. Отдельный кубит представляет собой два электрона, помещенные в двойные квантовые точки так, что половина электрона находится в одной точке, а другая его половина – в другой. Электрон может находиться в симметричном либо антисимметричном состоянии по отношению к операции перестановки точек. Вычисления основываются на переходах между этими состояниями, при этом перемещение электрона между точками не происходит. Базовым состояниям кубита (|0> и |1>) соответствует антисимметричное состояние одного электрона и симметричное состояние другого электрона, и наоборот. Внешние электроды управляют величиной туннельной связи между квантовыми точками и силой обменного взаимодействия. Поскольку последнее зависит от спиновой конфигурации, все электроны должны быть поляризованы. Добиться этого можно и без магнитного поля, например, доставлять электроны в квантовые точки с ферромагнитной частицы. Цепочка квантовых точек фактически представляет собой одноэлектронный насос. Для инициализации компьютера электроны накачиваются, а при считывании результата – выкачиваются. Чтобы отличить симметричное состояние электрона от антисимметричного, к квантовым точкам нужно приложить напряжение, при котором электрон перемещается либо в одну точку, либо в другую. В работе также показано, что вероятность индуцированных переходов электрона между симметричным и антисимметричным состояниями продолжает падать при уменьшении разности энергий этих состояний и только двухфононные процессы останавливают это падение, т.е. определяют предел достижимого времени декогеренизации в системе. Статья принята к публикации в первом номере нового международного журнала “Quantum Computers and Computing”.
Вначале напомним, что такое
вейвлет-преобразование. Оно является обобщением
дискретного преобразования Фурье (ДПФ), которое
широко используется, но дает равномерную ошибку
по частотам. Однако иногда требуется более точно
воспроизводить высокие частоты или низкие, или
вообще, средние. Можно, конечно, произвести
фильтрацию, что и делают. Но это приводит к потере
информации, преобразование перестает быть
обратимым. Эти недостатки преодолевает
вейвлет-преобразование. Предложено оно было
Haar’ом еще в 1910 году. Базис функций, по которому
производится разложение заданной функции f(x) для
получения ее вейвлет-образа fm строится
следующим образом. Сначала выбирается
материнский вейвлет y (x) на отрезке [0,1] и
строится набор дочерних вейвлетов y n(x,m)=2n/2y
(2nx-m). В отличие от ДФП это
преобразование содержит параметр n. На
материнский вейвлет накладываются два
ограничения: Как известно, быстрое ДПФ на классическом компьютере осуществляется за L? 2L шагов, где L- длина дискретного ряда. В то же время на квантовом компьютере это преобразование требует порядка L2 операций, т.е. приобретает экспоненциальное ускорение. Как показали недавние исследования, по отношению к вейвлет-преобразованию все обстоит так же (сказывается его родство с ДПФ). Подробнее о классическом вейвлет-преобразова-нии можно узнать из обзора Н.М.Астафьевой (УФН, №11, 1996).
Облако атомов натрия охлаждается лазерным способом до температуры 200мкК. Мягкая посадка облака на поверхность GaAs (но не вплотную) осуществляется с помощью магнитного поля, формируемого системой проводников с током. Атомы натрия имеют магнитный момент, и их движение обусловлено магнитным полем. Ток включается на короткое время, чтобы избежать разогрева газа, но этого времени достаточно для захвата облака атомов. После выключения магнитной ловушки включается ток в тонких золотых нитях (10мкм), расположенных на поверхности полупроводника. Магнитное поле этих нитей захватывает атомы. Перемещение атомов вдоль нити обусловлено их тепловым движением. При температуре 200мкК их тепловая скорость составляет 0.5м/с. С помощью люминесценции за этим перемещением можно легко наблюдать. Согласно теореме Ирншоу, любая магнитная и электрическая ловушка - “дырявая” (теорема утверждает, что гармоническая функция, которой описывается статическое электрическое и магнитное поле, не может иметь экстремумов). Поэтому происходит постоянный отсев захваченных атомов. Тем не менее, достаточное их количество послушно препровождается в заданное место. Исследователям удалось довести атомы до места раздвоения нити и увидеть разделение атомов на два пучка. Это пока все, что наблюдалось. Но перспективы вдохновляют. Можно надеяться увидеть в дальнейшем бозе-конденсацию атомов, релеевское рассеяние и интерференцию материальных волн, что пока было обнаружено только в больших магнитных ловушках с лазерным охлаждением (ПерсТ, вып. 3 с.г.). Очень заманчивой выглядит идея каналирования атомов в определенные места на подложке для формирования структуры квантового компьютера. Это и был бы атомный чип! В.Вьюрков http://xxx.lanl.gov/abs/quant-ph/0003135
Схем телепортации квантовых состояний уже было предложено огромное количество. Ученые из Clarendon Laboratory, University of Oxford и Blackett Laboratory, Imperial College (Англия) считают, что изобретенная ими схема телепортации является наиболее реалистической и обеспечивает большую вероятность успешной телепортации. Мотивация практической ценности их работы ясна. Квантовую информацию лучше записывать и обрабатывать на атомных состояниях или им подобных, поскольку там она может достаточно долго храниться. А вот передавать эту информацию лучше всего с помощью фотонов, которые могут быстро распространяться на большие расстояния без потери когерентности. Авторы рассматривают трехуровневый атом, у которого есть два вырожденных основных состояния и одно возбужденное. Атом помещается в микрорезонатор (cavity), обладающий собственной частотой несколько меньшей частоты резонансного возбуждения на верхний уровень. Такой же частотой обладает лазерный луч, освещающий микрорезонатор. Все это находится в распоряжении Алисы. Точно такая же установка у Боба. Требуется передать состояние атома Алисы, представляющего собой смесь основных состояний атома, на атом Боба. Для этого требуется еще одно устройство, а именно делитель (S), на который попадают фотоны, выходящие из микрорезонатора Алисы и Боба, а также детекторы фотонов D+ и D-, находящиеся в распоряжении Алисы (рис.1).
Далее в один и тот же момент времени Алиса и Боб включают лазеры на определенный промежуток времени, но разный у Алисы и Боба, а затем Алиса ждет щелчка детектора и сообщает Бобу (по телефону), какой детектор сработал. В зависимости от этого Боб определяет, получил ли он состояние атома Алисы или для этого надо еще произвести простейшую унитарную операцию (поворот фазы) над его атомом. Запутывание состояний атомов, необходимое для телепортации, происходит в момент срабатывания детектора, т.е., измерения, производимого над системой фотонов. Phys. Rev. Lett., 1999, 83, p.5158 Нападающие и защитники на поле квантовых компьютеров
Совсем недавно японские ученые из компании SHARP попытались доказать, что реализация алгоритма Шора на квантовом компьютере вовсе и не дает экспоненциального ускорения. Напомним, что время выполнения классического алгоритма экспоненциально зависит от длины разлагаемого числа, а время выполнения квантового алгоритма, как предполагалось ранее, - степенным образом. На самом деле, как сам Шор, так и все математики, работающие в области квантовых алгоритмов, говорят о количестве операций. Хотя практически важно именно время расчета! Его и определили японцы [1]. Алгоритм Шора опирается на квантовое дискретное преобразование Фурье (ДПФ), которое выполняется на квантовом компьютере как чередующиеся друг за другом преобразования Адамара над отдельными кубитами и операции условного поворота фазы в одном кубите j в зависимости от состояния другого кубита к на угол (teta) =(pi) / 2k-j. Если число кубитов равно n, то минимальный угол равен (pi) /2n-1. Пусть на эту операцию мы затрачиваем время (tau) min, тогда на операцию поворота на угол (pi) /2 для соседних кубитов мы затратим время порядка (tau) =(tau) min 2n. Экспоненциальная зависимость, полученная японскими учеными, совершенно “забивает” преимущества алгоритма Шора во времени расчета. Этот абсолютно правильный математический результат представлял смертельную опасность для квантовых компьютеров! К счастью, сомнения продолжались недолго. Спасением мы обязаны сотруднику ФТИАН Леониду Федичкину. Он вспомнил о работе финских авторов, среди которых наиболее известна фамилия Ekert’а, опубликованной в 1996 году [2]. Они исследовали влияние шума на точность ДПФ. Как видно из ранее изложенного, такое преобразование требует экспоненциально большого (по отношению к числу кубитов n) динамического диапазона углов (teta) . Что будет, если поворот на малые углы забивается шумом? Оказалось, что это не страшно. Если требуемая точность выполнения ДПФ равна e , то требуемая точность операции фазового сдвига в состоянии кубита равна 2(epsilon) /n2. Таким образом, повороты на малый угол можно вообще не выполнять! Расчеты Федичкина показывают, что устранение операции поворота фазы на малые углы сохраняют полиномиальную зависимость времени выполнения алгоритма Шора от количества кубитов n. Жизнь квантового компьютера продолжается! Все, изложенное выше, обсуждалось 22 января в Физико-технологическом институте РАН на научном семинаре по квантовым вычислениям под председательством акад. К.А.Валиева. В.Вьюрков
Бозе-конденсация и сверхизлучение
Оптические аналогии можно продолжать и дальше вплоть до так называемого сверхизлучения. Интересно, что это явление рассмотрел Robert Dicke в 1954 году, еще до изобретения лазеров. Суть заключается в том, что в системе двухуровневых атомов, возбужденных независимым (некогерентным) образом, возникает когерентное состояние. Это обусловлено взаимодействием отдельных атомов посредством излучаемых фотонов, которое приводит к синхронизации излучения в мощный импульс макроскопически поляризованных фотонов. Этот импульс назван автором вспышкой сверхизлучения (superradiant burts). Важным практическим следствием этого эффекта явилась генерация гармоник оптического излучения в нелинейной среде, полученная в группе P.Franken'а в 1961. Несколько позже этой группе удалось продемонстрировать и четырех волновое смешивание. Почти через 40 лет (в 1995 году) этот эффект был воспроизведен на материальных волнах P.Meystre'ом с коллегами в University of Arizona (США). Они смешивали два бозе-конденсата, находящихся в разных электронных состояниях. В 1999 году четырех волновое смешивание наблюдали специалисты из National Institute of Standards and Technology (NIST) [1], использовав только один бозе-конденсат. Три волны с волновыми векторами P1, P2, P3 получались в результате брегговской диффракции конденсата на решетке, представляющей собой стоячую оптическую волну, а вот четвертая зарегистрированная волна с волновым вектором P4= P1- P2+ P3 возникала в результате нелинейного взаимодействия трех изначальных.
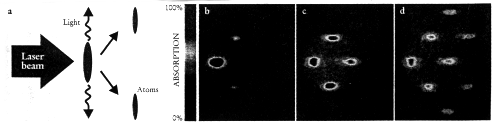
Совсем недавно эффекты смешивания оптических и материальных волн наблюдались группой ученых из Massachusets Institute of Technology (MIT), которую возглавляют W.Ketterle и D. Pritchard. Они наблюдали релеевское рассеяние лазерного пучка на бозе-конденсате атомов натрия, приготовленном в магнитной ловушке. Конденсат имел форму вытянутого эллипсоида. Обычное релеевское рассеяние в газе является изотропным, кстати, именно ему обязан голубой цвет неба. А вот в рассматриваемом эксперименте свет рассеивался преимущественно вдоль оси эллипсоида, а после отключения магнитного поля атомы конденсата разлетались в определенных направлениях (см.рис.). Последнее свидетельствовало о том, что эффект отдачи атомов в результате релеевского рассеяния не был хаотическим, как в обычном газе, а становился когерентным и приводил к образованию в конденсате стоячих материальных волн, на которых и рассеивались последующие фотоны. Отметим, что картинки b, c и d отличаются длиной волны лазерного излучения, соответственно 35, 75 и 100мкм. Как видно, соответвствующие частоты лазерных пучков далеки от частот резонансного возбуждения атомов. Авторы объяснили эксперимент квазиклассическими представлениями. Недавно M.G.Moore и P.Meystre построили квантовую теорию эффекта [3]. Настоящее обозрение в значительной степени основано на статье G.B.Lubkin [4].
Квантовый компьютер в полевом транзисторе
Двумя состояниями кубита являются наличие электрона в одной из спаренных точек. Управление туннелированием между этими точками, т.е. управление состоянием отдельного кубита, производится с помощью соответствующего затворного электрода, расположенного над спаренной квантовой точкой. Процесс туннелирования зависит также и от состояния соседних квантовых точек из-за кулоновского взаимодействия электронов, поэтому становится возможным выполнение и 2-х кубитных операций. Изюминкой работы является способ считывания конечного результата, для чего необходимо определить, в какой из спаренных квантовых точек находится электрон (в верхней или в нижней) в каждом кубите. Распределение электрического потенциала вдоль канала транзистора зависит от зарядового состояния спаренных точек, и, как показывает автор, по вольт-амперной характеристике транзистора можно “прочитать” это состояние. К сожалению, автор пока не знает или скрывает способ формирования предложенной структуры. http://xxx.lanl.gov/abs/quant-ph/990821
|
|||||||||||||||||||||




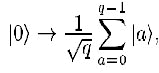 q=2^k.
q=2^k.

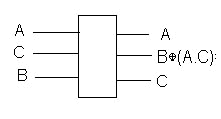
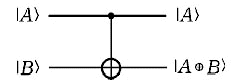 Низший бит
инвертируется всякий раз когда |A> =1
Низший бит
инвертируется всякий раз когда |A> =1 XOR гейт
позволяет перемещать информацию.
XOR гейт
позволяет перемещать информацию.