Справочное руководство по Electronics Workbench

Раздел: Цифровая схемотехника

Теоретическое введение:

Сумматор является простейшим цифровым устройством. Это узел ЭВМ, выполняющий арифметическое суммирование кодов чисел, т.е. он предназначен для сложения двух чисел, заданных в двоичном коде. Сравним суммирование десятичных и двоичных чисел:

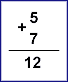Правила сложения двоичных и десятичных чисел одинаковы:

1. сложение производиться поразрядно – от младшего разряда к старшему;
2. в младшем разряде вычисляется сумма младших разрядов слагаемых А_i и В_i. Эта сумма в данной системе счисления может быть записана однозначным числом S₁ либо двухзначным числом P₁S₁. Функция P называется переносом;
3. во всех последующих разрядах находиться сумма данных разрядов слагаемых A_i и B_i, причем при P_i-1=1 к этой сумме добавляется единица (в числовых примерах, приведенных выше, этот случай выделен жирным шрифтом, результат сложения в i-м разряде записывается в виде однозначного S_i или двухзначного P_iS_i числа.

Таким образом, в каждом разряде необходимо найти сумму A_i, B_i и P_i-1 (если P_i-1=1), т.е. определить S_i и P_i. По числу входов различают полусумматоры, одноразрядные сумматоры (ОС) и многоразрядные сумматоры.

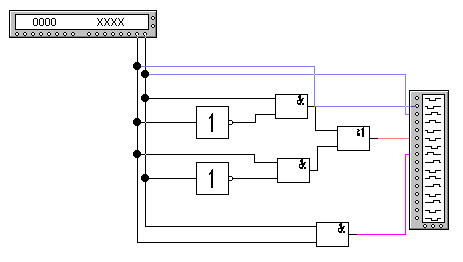
Рисунок 3.2.3.1 - Схема полусумматора

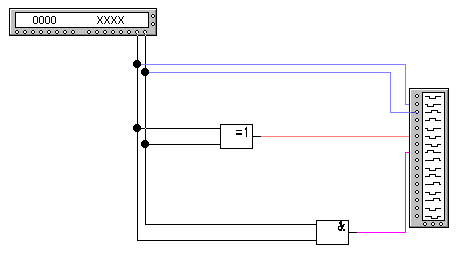
Рисунок 3.2.3.2 - Схема полусумматора с использованием стандартной схемы сложения по модулю 2

Полусумматорами называются устройства с двумя входами и двумя выходами, на которых вырабатываются сигналы суммы и переноса. Полусумматор реализует лишь часть задачи суммирования, так как не учитывает входной величины – переноса из соседнего младшего разряда в данных(см. рисунки 3.2.3.1 и 3.2.3.2). В таблице 3.2.3.1 приведена таблица истинности полусумматора. На рисунке 3.2.3.3 приведена временная диаграма работы полуссуматора.

Таблица 3.2.3.1 - Таблица истинности полусумматора

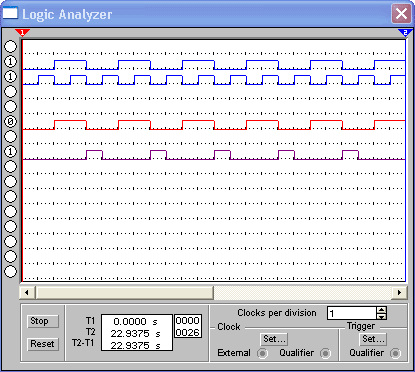
Рисунок 3.2.3.3 - Диаграмма работы полусумматора

Логические уравнения: S=x^*y+x*y^ P=x*y

Одноразрядный двоичный сумматор состоит из двух комбинационных схем: одна формирования S_i, вторая для определения P_i. (см. рисунки 3.2.3.4 и 3.2.3.5). Многоразрядный сумматор строится на основе одноразрядных в соответствии с правилами сложения.

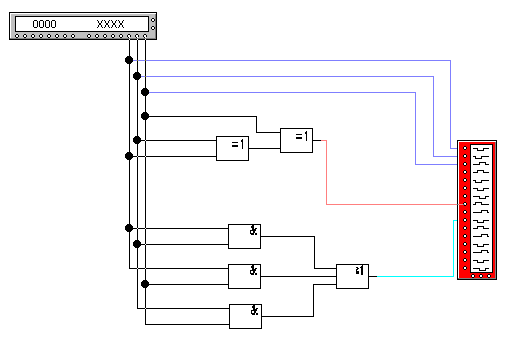
Рисунок 3.2.3.4 - Схема однорязрядного двоичного сумматора

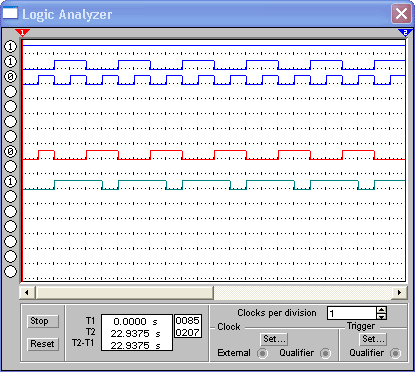
Рисунок 3.2.3.5 - Диаграмма работы однорязрядного двоичного сумматора

Одноразрядные сумматоры имеют три входа и обеспечивает сложение разрядов слагаемых и переносом из предыдущего разряда. (см. таблицу 3.2.3.2).

Таблица 3.2.3.2 - Таблица истинности сумматора

Логические уравнения
S=y1+y2+y3+y4
Y1=x1^*x2^*x3
Y2=x1^*x2*x3^
Y3=x2^*x3^*x1
Y4=x1*x2*x3
Pi+1=y1+y2+y3+y4
Y1=x1^*x2*x3
Y2=x1*x2^*x3
Y3=x1*x2*x3^
Y4=x1*x2*x3

Минимизируя данные уравнения по формулам алгебры логики, построим сумматор в Electronics Workbench.

В зависимости от характера ввода-вывода кодов и организации переносов многоразрядные сумматоры бывают последовательного и параллельного принципа действия.

В последовательном сумматоре сложение кодов осуществляется, поразрядно начиная с младшего разряда с помощью комбинационного сумматора на три входа. Образующийся в данном разряде перенос Рj+1 задерживается на время tэд и поступает на вход Pj сумматора в момент поступления следующего разряда слагаемых. Таким образом, последовательно разряд за разрядом производиться сложение кодов чисел. Достоинством последовательного сумматора является простота аппаратурной реализации, а недостатком - достаточно большое время суммирования (см. рисунок 3.2.3.6). На рисунке 3.2.3.7 приведена временная диаграмма, иллюстрирующая работу последовательного сумматора.

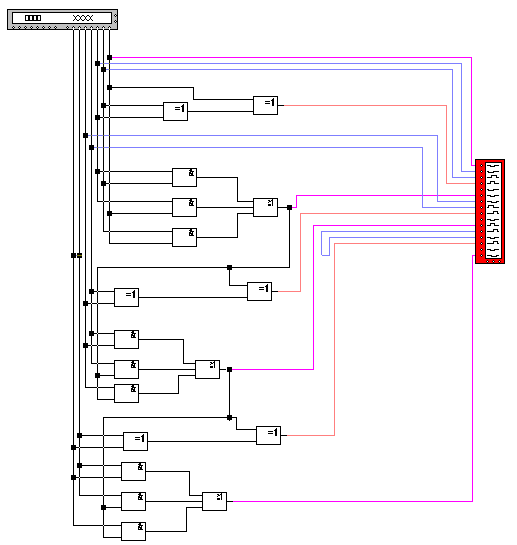
Рисунок 3.2.3.6 - Схема последовательного сумматора

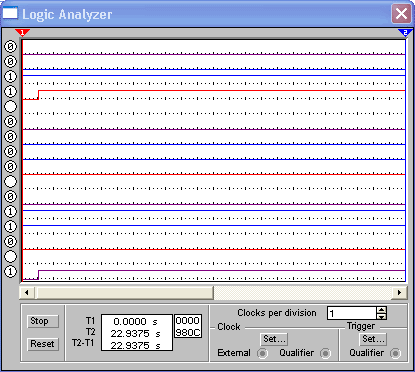
Рисунок 3.2.3.7 - Диаграмма работы последовательного сумматора

В параллельном сумматоре достигается более высокое быстродействие. Суммируемые коды поступают на входы сумматора одновременно по всем разрядам. Для этого в каждом разряде используется комбинационный сумматор на три входа, на выходах которого образуются значения суммы Sj данного разряда и переноса Pj+1 в старший разряд. В процессе распространения сигнала переноса устанавливается окончательное значение суммы в каждом разряде. Очевидно, что в течение этого времени на входах сумматора присутствуют сигналы Xi, Yi, соответствующие суммируемым кодам. Максимальное по времени суммирование получается в том случае, когда перенос, возникший в первом разряде, распространяется по всем разрядом (например, при сложении кодов 11..11 и 00..01). В параллельном сумматоре обычно применяются различные способы ускорения переноса (параллельный перенос, групповой и т. п. На, приведена временная диаграмма, илылюстрирующая работу последовательного сумматора.

Цифровые схемы сравнения формируют на выходе F=1 при равенстве подаваемых на вход двух двоичных чисел А (поразрядно записываем a и b) и В (c и d). Цифровая схема сравнения это цифровой аналог компаратора (см. рисунок 3.2.3.8), являющегося одним из важнейших устройств импульсной техники, временная диаграмма сумматоров приведена рисунке №2.3.9, приложения. На основе таблицы истинности для компаратора составим уравнения (для A>B, A<B, A=B), минимизируем их используя законы алгебры логики (см. таблицу №2.3.3, приложения).

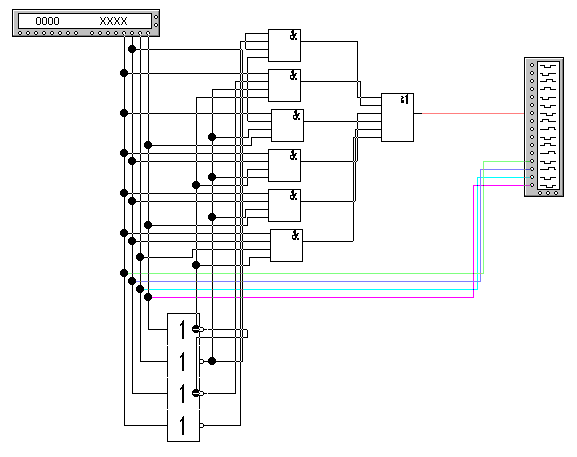
Рисунок 3.2.3.8 - Цифровая схема сравнения

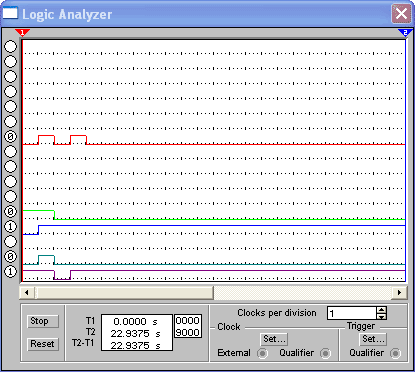
Рисунок 3.2.3.9 - Диаграмма работы цифровой схемы сравнения

Таблица 3.2.3.3 - Таблица истинности цифровой схемы сравнения

Логические уравнения:

A>B = a^bc^d^ + ab^c^d^ + ab^c^d + abc^d^ + abc^d + abcd^
A<B = a^b^c^d + a^b^cd^ + a^b^cd + a^bcd^ + a^bcd + ab^cd
A=B = a^b^c^d^ + ab^cd^ + a^bc^d + abcd

Задание:

1. Используя пакет Electronics Workbench спроектировать схему на основе простейших элементов, используя для составления схемы таблицу истинности и проанализировать работу сумматора или схемы сравнения.
    
2. Составить отчет о выполнении лабораторной работы в MS Word в котороый включить:
   - схемы построенные в Electronics Workbench;
   - временные диаграммы работы выполненых вами схем.

- Спроектировать однорозрадный сумматор.

1. Спроектировать четырехразрядный сумматор с последовательным переносом;
2. Спроектировать цифровую схему сравнения двухразрядных двоичных чисел А<B;
3. Спроектировать цифровую схему сравнения двухразрядных двоичных чисел А>B
4. Спроектировать цифровую схему сравнения двухразрядных двоичных чисел А=B;